Estratégias Fraudulentas para a Roleta e Porque Não Funcionam
- Estatisticamente, porque é que os jogadores perdem dinheiro em cada aposta que fazem na roleta?
- Estratégias que não funcionam na roleta
- Estratégia de Martingale para a roleta
- Estratégia de Fibonacci para a roleta
- Estratégia de D'Alembert para a roleta
- Estratégia de Labouchere para a roleta
A roleta é um dos jogos de casino mais populares do mundo. Isso significa que, além de outras coisas, pode encontrar online uma enorme quantidade de conteúdos sobre este jogo. Parte do conteúdo é legítimo e apresenta as coisas como realmente são. No entanto, existem imensos websites que tentam enganar as pessoas e levá-los a jogar roleta pensando que vão realmente ganhar dinheiro a longo prazo.
Infelizmente, isso não é possível. A longo prazo, é impossível "derrotar" uma roleta a funcionar adequadamente, e continuar a ganhar dinheiro ao casino. A incapacidade de vencer a roleta está profundamente enraizada nos fundamentos matemáticos e estatísticos do jogo. Aprofundaremos isso mais tarde.
Continue a ler este artigo para descobrir a razão pela qual é impossível vencer a roleta e porque as estratégias de roleta frequentemente apresentadas com a promessa de ganhos consistentes simplesmente não funcionam. Espero ensinar-lhe quais as estratégias a evitar e porquê, para que não se deixe enganar pelas informações muito tentadoras, mas muitas vezes enganosas, que podem ser encontradas online.
Considero as estratégias apresentadas neste artigo fraudulentas, porque geralmente prometem aos jogadores ganhos consistentes, o que é uma promessa que simplesmente não é possível cumprir. Contudo, pode aplicar algumas estratégias para jogar roleta da forma mais eficiente possível e, na verdade, maximizar as suas hipóteses de sair do casino com lucro. Saiba mais sobre elas no meu artigo sobre as estratégias de roleta que funcionam.
Estatisticamente, porque é que os jogadores perdem dinheiro em cada aposta que fazem na roleta?
Gostaria de começar por explicar o motivo pelo qual todas as apostas feitas numa mesa de roleta fazem com que o jogador perca dinheiro a longo prazo. Como já mencionei, isso está relacionado com as probabilidades da roleta e a forma como o jogo funciona do ponto de vista matemático.
RTP e margem da casa na roleta
Todos os jogos de casino podem ser caraterizados pelo chamado 'retorno para o jogador' (RTP), que descreve a percentagem de cada aposta que, estatisticamente, retorna ao jogador. Se um determinado jogo tivesse um RTP de 100%, as hipóteses de ganhar ou perder seriam as iguais. Porém, os jogos de casino têm quase sempre (excluindo algumas exceções raras) um RTP mais baixo.
A roleta não é uma exceção. O RTP da roleta Europeia é 97.3%, ao passo que o RTP da roleta Americana é 94.74%. Isso significa que, se um jogador apostar $100, estatisticamente, ganha $97.30 na roleta Europeia ou $94.74 na roleta Americana. Como estes ganhos são inferiores às apostas originais, é bastante claro que o jogador perde dinheiro em cada aposta na roleta.
A margem da casa é a vantagem que o casino tem sobre os jogadores. Pode ser calculado como:
Margem da casa = 100 - RTP
Isto significa que a margem da casa da roleta Europeia é de 2.7% e que a margem da casa da roleta Americana é de 5.26%. Por outras palavras podemos afirmar que a longo prazo, por cada $100 apostados por um jogador, o casino ganha $2.70 na roleta Europeia e $5.26 na roleta Americana.
Esteja à vontade para ler mais sobre este assunto no meu artigo sobre as probabilidades da roleta, que inclui o RTP e a margem da casa deste jogo.
O que precisa saber para entender este artigo é que não há forma de vencer a roleta, porqueestatisticamente, perde dinheiro a cada aposta que faz, independentemente do tipo e do montante da aposta. Não há como contornar esta realidade.
Estratégias que não funcionam na roleta
Chegou finalmente a hora de abordar estratégias específicas para roleta que na realidade não funcionam, mas muitas vezes são apresentadas como uma maneira infalível de ganhar dinheiro num casino.
Para cada uma das estratégias fraudulentasapresentadas abaixo, explicarei:
- Como deve funcionar a estratégia e como é utilizada
- O porquê da estratégia não funcionar e porque irá custar-lhe dinheiro
- Simulações da estratégia que está sendo descrita, que demonstram claramente que o único resultado plausível a longo prazo é a perda de dinheiro
O que torna estas estratégias tão populares
Muitos websites apresentam estas estratégias como uma forma infalível de ganhar dinheiro online, pois o seu único objetivo é conseguir que novos jogadores se registem num casino online utilizando o link fornecido, permitindo assim que o website ganhe dinheiro. Não se importam com o facto de estarem a mentir aos seus leitores. Além disso as estratégias fraudulentas apresentadas neste artigo podem ser muito tentadoras à primeira vista, especialmente quando são apresentadas informações enganosas.
É precisamente por esse motivo que estas estratégias são glorificadas por um número tão grande de websites, e é precisamente por isso que deve ler todas as informações sobre esse tipo de estratégias que podem ser descritas noutros websites como a última bolacha do pacote.
Estratégia de Martingale para a roleta
Entre as estratégias fraudulentas para a roleta, a estratégia de Martingale é sem dúvida a mais popular (também conhecida como a estratégia da duplicação na roleta). Esta estratégia é muito simples, o que pode ajudar à popularidade, já que praticamente qualquer pessoa pode utilizá-la sem fazer qualquer pesquisa ou estudo.
A estratégia de Martingale funciona da seguinte forma:
- O jogador faz uma aposta inicial, por exemplo $1, em qualquer uma das apostas 50/50 (vermelho/Preto, par/impar, alto/Baixo). A aposta na cor vermelha/preta é a mais utilizada, mas estatisticamente não existe qualquer diferença entre as várias apostas 50/50.
- Se o jogador ganhar, volta ao ponto de partida e aposta $ 1 novamente. Se perder, duplica a sua aposta. Este procedimento é repetido até o jogador ganhar. Posteriormente, o jogador retorna ao ponto de partida e aposta novamente $1.
A estratégia de Martingale funciona por ciclos. A duração de cada ciclo individual varia, mas no final de cada ciclo o jogador deve ganhar $1 ou perder tudo. Começamos com os casos vencedores e falamos sobre as perdas mais tarde.
Aqui estão alguns exemplos dos ciclos vencedores da estratégia de Martingale:
- O jogador aposta $1 e ganha $2. O ganho líquido é de $1.
- O jogador aposta $1 e perde. De seguida aposta $2 e ganha $4. No total o jogador aposta $3 e ganha $4. O ganho líquido é de $1.
- O jogador aposta $1 e perde. Posteriormente o jogador aposta $2, $4, $8, $16, $32, $64, $128, $256 e perde todas estas apostas. De seguida aposta $512 e ganha. A aposta total foi de $1023 e o retorno de $1024. O ganho líquido é de $1.
Todos estes casos foram bem-sucedidos para o jogador, mas como provavelmente já percebeu, o último caso foi muito pior que os dois primeiros. O jogador perdeu por nove vezes consecutivas, ganhando apenas à décima aposta. Isto significa que teve de apostar $512 para ganhar apenas $1 em todo o ciclo. O incremento rápido do tamanho das apostas é um dos principais problemas da estratégia de Martingale.
O que faz com que estratégia de Martingale aparente funcionar
Há uma explicação lógica muito boa para o porquê da estratégia de Martingale funcionar. Se continuar a duplicar a sua aposta inicial, a bola da roleta deve, mais cedo ou mais tarde, cair num número que lhe garanta uma vitória. Certo?
Sim, isso é verdade. À medida que o número de tentativas aproxima-se de infinito, a probabilidade de perder tudo aproxima-se de 0. Isto significa quecom recursos infinitos e sem limitações do casino, acabará conseguindo vencer e encerrar um ciclo com ganhos líquidos de $1.
Com recursos infinitos recursos e sem limitações do casino, todo o sistema funcionaria. Contudo, como provavelmente já se apercebeu, estas duas condições nunca se verificam no mundo real. Vamos aprofundar estes problemas.
Problema #1: Banca limitada
No mundo real, todos os jogadores têm uma banca limitada. Isto significa que se um jogador continuar a utilizar a estratégia Martingale a longo prazo, eventualmente ficará sem dinheiro, tornando-o incapaz de fazer outra aposta e terminar um ciclo vencedor.
Vamos analisar esta situação utilizando um exemplo. Imagine um jogador com uma banca de $1.000 a utilizar a estratégia de Martingale com uma aposta inicial de $1. Com uma banca de $1000, o jogador será capaz de colocar sucessivamente as seguintes apostas: $1, $2, $4, $8, $16, $32, $64, $128, $256. A soma total destas apostas é de $511, o que significa que, depois de perder todas estas apostas, o jogador terá apenas $489 na sua conta, sendo impossível fazer a aposta seguinte, no valor de $512.
No entanto, para o efeito dos meus cálculos, decidi deixar esse facto de fora e considerar o caso descrito acima como uma falha. Ainda assim, nas minhas simulações - que pode encontrar mais adiante neste artigo - permito que os jogadores simulados continuem apostando todo o seu saldo quando não tiverem dinheiro suficiente para acompanhar o tamanho das apostas, conforme determinado pela estratégia de Martingale.
Agora pode achar que é muito improvável que isso aconteça. Para este cenário se tornar realidade, o jogador tem de perder 9 apostas consecutivas. À primeira vista, pode parecer que isso nunca acontece, no entanto, acontece. E acontece com mais frequência do que possa pensar.
Na roleta Europeia, a probabilidade de perder uma apostas 50/50 durante 9 vezes consecutivas é:
(19/37)^9 = 0.0025 = 0.25%
Sim, é um valor baixo. Contudo, esta probabilidade significa que estatisticamente, 1 em cada 402 ciclos de Martingale resultarão em 9 apostas consecutivas perdidas, levando a que o jogador não consiga continuar a apostar.
É claro que, depois de aumentar sua banca para $1023, o jogador pode perder 9 apostas seguidas, e terá dinheiro suficiente para fazer a 10ª aposta de $512 após perder todas as apostas anteriores. Ao atingir este nível, apenas em 1 a cada 784 ciclos não terá saldo suficiente para fazer outra aposta.
Com uma banca suficiente a probabilidade de perder um ciclo é, portanto, bastante baixa. Porém, para ganhar dinheiro consistentemente utilizando a estratégia de Martingale, precisará de repetir todo o processo milhares de vezes, o que significa que mais cedo ou mais tarde perderá toda a sua banca. As simulações da estratégia de Martingale que encontrará mais adiante neste artigo demonstrarão claramente este facto.
Problema #2: Limites aos montantes das apostas
Além dos problemas com a banca, a estratégia de Martingale é também limitada pelos montantes máximos das apostas do casino onde está jogar . Obviamente, os limites mínimo e máximo da mesa diferem entre diferentes casinos e jogos. Mas, de um modo geral, a aposta máxima permitida geralmente é apenas algumas centenas de vezes maior que a aposta mínima.
Ao jogar em casinos online, geralmente pode usar vários jogos de roleta online com diferentes limites para superar essas limitações. Isto não é muito prático, mas pode ser utilizado para minimizar o impacto dos limites aos montantes das apostas na eficácia da estratégia de Martingale.
E, mesmo utilizando várias mesas de roleta para contornar estes limites, a sua aposta máxima continua a ser limitada. Portanto, mesmo que tivesse uma banca infinita (o que significa que não seria afetado pelo problema # 1), estaria limitado pela aposta máxima permitida na roleta que escolhesse jogar.
Problema #3: Saber quando parar
Como já deve ter notado, a probabilidade de perder 9 ou 10 apostas seguidas num ciclo é bastante baixa. Até mesmo perder 1 em cada 100 ciclos é pouco provável. Na verdade, se tivesse uma banca que lhe permitisse fazer 10 apostas consecutivas após perder todas as apostas anteriores (de $1023 a $2046) e quisesse ganhar apenas $100, a probabilidade de sucesso seria:
(1-(19/37)^10)^100 = 0.88 = 88%
Assim, com o objetivo de ganhar $100, teria uma probabilidade de sucesso de 88%. Nos 12% restantes, acabaria perdendo uma parte significativa da sua banca e não conseguiria fazer outra aposta.
Se a meta for $200, as suas hipóteses de atingir o objetivo serão de 77,5%, com uma meta de $500 baixará para 52,8% e com uma meta de $1.000, será de 27,9%. Como pode ver, a probabilidade de sair como vencedor diminui quanto mais alta for a meta estabelecida, o que é algo lógico.
O problema #3 da estratégia de Martingale reside no facto da estratégia ter a tendência de funcionar a princípio, o que faz com que os jogadores se tornem excessivamente confiantes, pensando que a estratégia continuará funcionando para sempre. Infelizmente, não é o caso. Se continuar usando a estratégia Martingale por tempo suficiente, acabará por perder toda a sua banca.
Se os jogadores soubessem reconhecer o momento certo para sair do casino, a maioria acabaria com lucro. No entanto, não há um momento ideal para parar de jogar, porque não há como antecipar uma sequência de derrotas. Além disso, não existe a garantia que o jogador não vai perder tudo no primeiro ciclo da estratégia de Martingale.
Simulações da estratégia de Martingale
Simulei 5 jogadores a utilizar a estratégia Martingale enquanto jogavam numa roleta Europeia. Aqui está tudo o que precisa saber sobre as simulações:
- Cada jogador começou com uma banca de $1000 e a aposta inicial foi de $1.
- As simulações são interrompidas após 10.000 rondas ou quando os jogadores perdem toda a sua banca.
- Os jogadores seguiram a estratégia do Martingale e fizeram suas apostas em concordância.
- Se os jogadores não tinham dinheiro suficiente para fazer a aposta seguinte, apostavam todo o seu saldo restante. Se perderem essa aposta, a sua aventura termina. Se vencerem, continuam de acordo com a estratégia da Martingale e apostam $1 na ronda seguinte.
- Criei as simulações utilizando meu próprio software de simulação, que faz uso de um RNG (Random Number Generator) para determinar o resultado da ronda. Isto é valido para todas as simulações deste artigo. Na roleta, os números aleatórios são gerados pela própria roleta, mas do ponto de vista estatístico os resultados são os mesmos.
Vejamos os resultados:
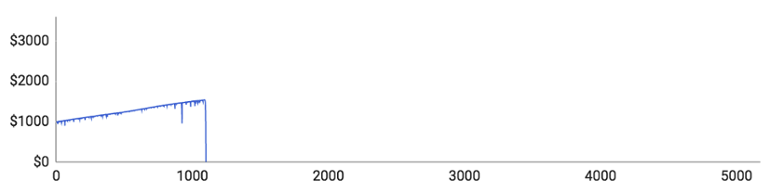
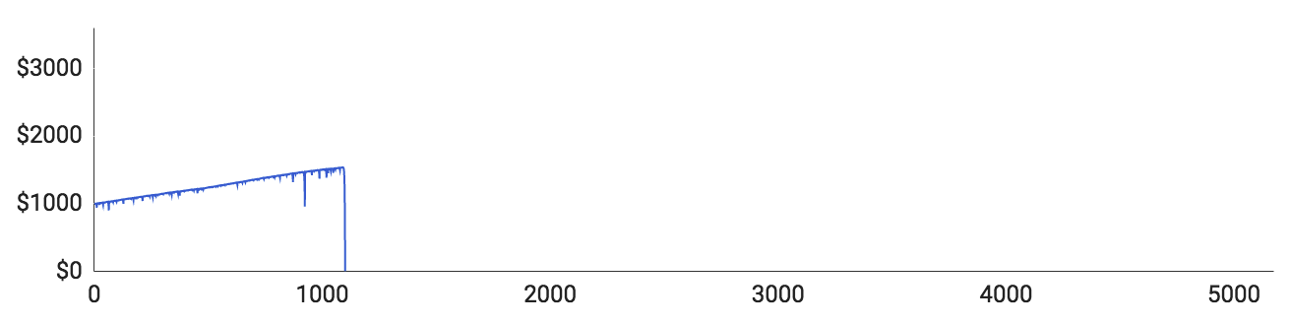
Como pode ver, todos os jogadores perderam por completa a sua banca antes de atingir as 10,000 rondas. Vamos analisar os jogadores individualmente e ver como eles se saíram:
- O Jogador #1 estava numa maré de sorte no começo e conseguiu aumentar sua banca até aos $1500, com apenas uma sequência de derrotas mais longa. No entanto, ele perdeu 11 rondas consecutivas, o que levou a sua banca de $1540 a $ 0.
- O Jogador #2 teve muito menos sorte. Apenas 51 rondas foram o suficiente para perder toda a sua banca. É uma ocorrência bastante rara, mas mostra claramente que as coisas podem correr muito mal desde o início.
- O Jogador #3 acabou perdendo a sua banca em 417 rondas. Encontrou uma longa sequência de derrotas, da qual recuperou, mas perdeu 11 rondas seguidas pouco depois.
- O Jogador #4quase perdeu tudo na ronda 193, após a qual ficou com apenas $70. A partir daí começou uma recuperação e conseguiu que a sua banca atingisse os $477. Nessa altura deparou-se com uma sequência de derrotas que o fizeram bater nos $0.
- O Jogador #5 foi o que teve mais sorte, mas ainda assim não consegui sair com dinheiro da simulação. Ele chegou a atingir os $3308. Depois disso, perdeu 12 rondas consecutivas e ficou sem nada.
Isto demonstra que, a longo prazo, a estratégia de Martingale não funciona. Todos os jogadores estavam subindo lentamente, mas experimentaram uma série de derrotas brutais que resultaram na perda de tudo. Isto demostra que as longas séries de perdas, embora pareçam realmente improváveis são, na realidade, bastante comuns.
Estratégia de Fibonacci para a roleta
Apesar de existirem algumas semelhanças entre as estratégias de Fibonacci e de Martingale, existem também algumas diferenças. Vou focar principalmente os pontos nos quais estas duas estratégias diferem.
Em primeiro lugar, vamos descrever o funcionamento da estratégia de Fibonacci. Toda a estratégia está baseada na famosa sequência de números de Fibonacci. A sequência avança da seguinte forma:
1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 - 89 - 144 - 233 - 377 - 610 - 987 ...
Deve ter reparado (ou talvez já sabia de antemão) que cada número desta sequência é a soma dos dois números anteriores. Esta propriedade da sequência é utilizada na estratégia, embora possa não ser perceptível ao princípio.
A estratégia de Fibonacci para a roleta é utilizada da seguinte forma:
- O jogador começa apostando um valor correspondente ao primeiro número da sequência.
- Sempre que perde, avança para o próximo número na sequência e aposta o valor correspondente. Sempre que ganha, recua duas posições na sequência de números. Se o jogador voltar ao início da sequência, continua apostando uma quantia correspondente ao primeiro número até perder; a partir daí continua em conformidade.
Esta estratégia não é tão fácil de seguir como a estratégia de Martingale. Aqui estão alguns exemplos que podem ajudá-lo a entender o seu funcionamento.
- O jogador aposta $1 e ganha. O ciclo está completo e recomeça do início da sequência.
- O jogador aposta $1 e perde. Então, aposta novamente $1 (mas neste caso a aposta corresponde ao segundo número na sequência, não o primeiro - é importante compreender estas distinção) e ganha. O jogador deveria recuar dois números, mas existe apenas um número (1). Então ele recua para esse número e prossegue apostando novamente $1. Se ele ganhar, completa um ciclo e pode recomeçar do início.
- O jogador aposta $1 e perde. Em seguida aposta $1, $2, $3, $5, $8, $13, $21 e $34, e perde todas estas apostas. Na aposta seguinte, aposta $55 e ganha finalmente. Isto significa que o jogador recua para a aposta de $21 e continua a apostar de acordo com a estratégia.
Vantagens e desvantagens da estratégia de Fibonacci
Existe uma grande diferença entre as estratégias de Fibonacci e Martingale para a roleta. Na estratégia de Martingale uma única vitória é suficiente para completar um ciclo vencedor. Por outro lado, na estratégia de Fibonacci, o jogador completa um ciclo de vitórias apenas quando consegue voltar ao início da sequência e vencer a aposta correspondente ao seu primeiro número. Por outras palavras, uma vitória não é suficiente para inverter uma série de perdas.
Isto significa que a estratégia de Fibonacci precisa de um número maior de rondas da roleta para obter os mesmos ganhos comparativamente à estratégia de Martingale. Isto significa também que a estratégia de Fibonacci é menos arriscada.
Simulações da estratégia de Fibonacci
As simulações da estratégia de Fibonacci foram feitas nos mesmos termos que as simulações da estratégia de Martingale. A única diferença foi a estratégia utilizada pelos cinco jogadores simulados.
Vejamos os resultados:

Os gráficos são bastante semelhantes aos gráficos dos jogadores que usam a estratégia Martingale, mas existem algumas diferenças:
- Os gráficos crescem a uma ritmo ligeiramente mais baixo. Este comportamento é consistente com o facto da estratégia de Fibonacci ser menos arriscada e serem necessárias mais rondas para obter o mesmo lucro.
- Os gráficos de estratégia de Fibonacci são mais variados. Com a estratégia de Martingale, a banca individual continua crescendo aproximadamente ao mesmo ritmo, até cair para zero. Por outro lado, a banca dos jogadores que usam a estratégia Fibonacci tem um oscilação maior, pois uma aposta vencedora não é suficiente para quebrar uma série de perdas.
Vamos agora observar os resultados individuais dos jogadores:
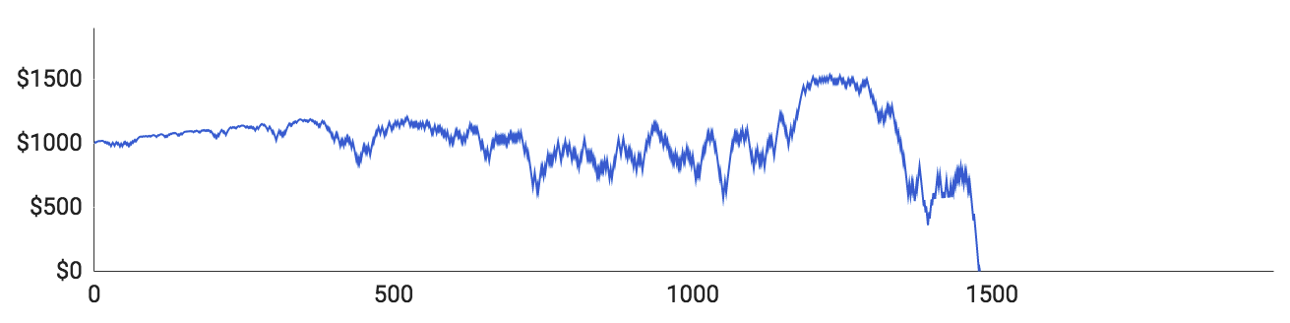
- O Jogador #1 foi o primeiro a perder toda a sua banca. Foram necessárias 488 rondas para perdê-la e em nenhum momento ele conseguiu obter um lucro substancial. O valor mais alto da sua banca foi de $1074. No final, 11 rondas perdidas fizeram-no cair de $1067 para $0.
- O Jogador #2 esteve melhor. Foram necessárias 2291 rondas para perder toda a sua banca, que chegou a atingir os $1330, que ele alcançou 27 rondas antes de ficar sem dinheiro. Nas últimas 27 rondas, ele venceu apenas 4 e perdeu as restantes 23, o que significa que suas apostas continuavam aumentando e ele continuava perdendo cada vez mais rápido.
- O Jogador #3 jogou 4290 rondas, mas a sua banca nunca ultrapassou os $1298, que fica abaixo do pico da banca do Jogador # 2. Isto deve-se ao facto de ter perdido quase tudo no início da simulação, o que significa que ele tinha que apostar tudo com apenas $122 na sua 656ª ronda. Ainda assim conseguiu vencer essa ronda e começou a recuperar lentamente, mas mais tarde foi atingido por uma onda de perdas que o fez perder tudo.
- O Jogador #4 perdeu toda a sua banca em 1272 rondas. A sua banca atingiu os $1175. Ele teve que ir "all-in" com $145 na 1176ª ronda e conseguiu vencer, mas perdeu tudo nas 100 rondas seguintes.
- O Jogador #5 teve a melhor prestação de todos. Jogou 7132 rondas e a sua banca atingiu o valor mais alto: $2269. Infelizmente, ele não conseguiu chegar à marca de 10.000 rondas, porque também teve uma sequência de derrotas que fizeram a sua banca cair para $0.
Em suma, a estratégia de Fibonacci é, em muitos aspetos, semelhante à estratégia de Martingale, mas tudo cresce e decresce a um ritmo mais lento. A banca aumenta mais lentamente, mas os tamanhos das apostas também aumentam mais lentamente quando se depara com uma sequência de derrotas. É por isso que, em média, os jogadores jogaram mais rondas e, ao mesmo tempo, a sua banca não atingiu valores tão altos como os obtidos quando usavam a estratégia de Martingale.
Estratégia de D'Alembert para a roleta
As estratégias de Martingale e Fibonacci funcionam aumentando ou diminuindo a quantia apostada, em função do resultado das rondas individuais. O sistema de apostas de D'Alembert funciona de modo semelhantes, mas as diferenças nos montantes apostados são muito menores. Por esse motivo esta estratégia é muito mais segura.
A estratégia D'Alembert para a roleta baseia-se em apostas 50/50 (vermelho/preto, par/impar e alto/baixo) Funciona desta forma:
- O jogador decide o valor da sua aposta inicial e faz a aposta.
- Sempre que o jogador perde, aumenta o valor apostado em uma unidade na ronda seguinte. Sempre que o jogador ganha, diminui o valor apostado em uma unidade na ronda seguinte.
Digamos que o jogador escolheu uma aposta inicial de $6 e começa a apostar. Aposta $6 e perde. Aposta $7 e perde. Aposta $8 e ganha. Aposta $7 e perde. Aposta $8 e ganha. Aposta $7 e ganha. Ao todo, o jogador fez 6 apostas, das quais ganhou 3 e perdeu 3. Mesmo tendo vencido o mesmo número de apostas que perdeu, consegue lucrar $3. É exatamente assim que a estratégia funciona.
Quando um jogador utiliza a estratégia de D'Alembert na roleta, vencer o mesmo número de rondas que perdeu garante lucro, definido pelo número de rondas ganhas/perdidas. Se ele ganhou 10 rondas e perdeu 10 rondas, terá um lucro de $10, independentemente do tamanho da aposta inicial.
Isso pode parecer ótimo, porque parece interessante por ser necessário um número igual de rondas ganhas e perdidas para obter lucro. No entanto, nas apostas 50/50 as suas hipóteses de ganhar não são 50:50 (apesar do seu nome). Na realidade, estatisticamente, ganhará apenas 48,65% das rondas e perderá as 51,35% restantes na roleta Europeia. Esta diferença é suficiente para impedir que a estratégia de D'Alembert seja lucrativa a longo prazo.
Vantagens e desvantagens da estratégia de D'Alembert
A vantagem deste sistema de apostas reside no facto de ser muito menos arriscado do que os sistemas de Martingale e Fibonacci. Obviamente, ainda existem riscos envolvidos, mas como as apostas aumentam lentamente durante a sequência de derrotas, não requer uma banca tão grande. É menos provável que perca toda a sua banca e provavelmente não terá problemas com as apostas máximas e mínimas da mesa de roleta.
Por outro lado, a progressão lenta do tamanho das apostas também pode ser uma desvantagem. Em primeiro lugar não ganhará muito dinheiro utilizando esta estratégia, pelo menos ao considerar sua aposta inicial e o número de rondas que precisa de jogar.
Além disso, ao deparar-se com uma sequência de derrotas, verá que é muito difícil voltar ao verde. Na verdade, precisa de uma sequência de vitórias comparável para o conseguir. Comparativamente a outras estratégias, na estratégia de Martingale, precisa de apenas de vencer uma ronda para quebrar a sequência de derrotas. Na estratégia de Fibonacci precisa de um pouco mais que isso, mas ainda assim não tanto como precisa no sistema de D'Alembert.
Simulações da estratégia de D'Alembert
Ao simular a estratégia de D'Alembert, reparei que não podia definir a aposta mínima em $1, uma vez que é suposto as apostas ficarem mais pequenas quando os jogadores estão a ganhar. Se a aposta inicial fosse de $1, não haveria espaço para as apostas ficarem menores. Ao mesmo tempo, não quero aumentar muito mais, para que os resultados sejam comparáveis.
Assim sendo, defini uma aposta inicial de $5 para esta estratégia, começando os jogadores com uma banca de $1000. Os jogadores seguiram a estratégia D'Alembert e, ao fazer uma aposta de $1, continuam apostando $1 até perder uma ronda e a sua aposta aumentar.
Aqui estão os resultados:
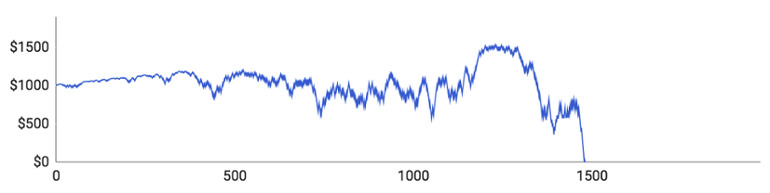
Vamos analisar os resultados individuais:
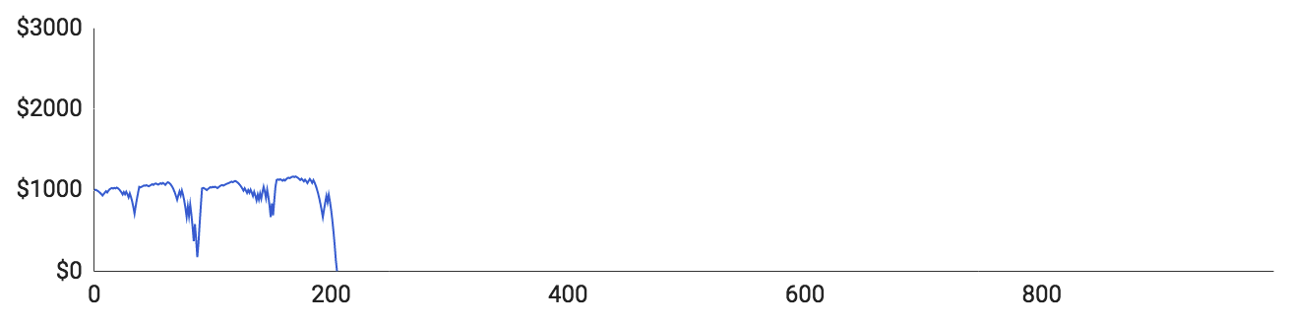
- O Jogador #1 consegui jogar 1480 rondas antes de ficar sem dinheiro. A sua banca atingiu os $1532. O tamanho de suas apostas continuava crescendo, o que significava que as subidas e descidas também estavam ficando cada vez maiores. A aposta máxima feita por ele foi de $58 e aposta média por ronda fixou-se nos $23.40.
- O Jogador #2 conseguiu os melhores resultados. Ao todo jogou 1971 rondas e conseguiu levar a sua banca até aos $1824. Porém, deparou-se com uma sequência de derrotas que o fizeram cair para $0. A sua aposta máxima foi de $62, mas a aposta média situou-se nos $16.75, porque a sua performance estava acima da média e, por esse motivo, as suas apostas permaneceram pequenas.
- O Jogador #3 jogou apenas 406 rondas e teve uma prestação fraca. Ganhou apenas 184 das 406 rondas (45,3%), o que é significativamente pior do que o valor esperado: 48,65%. A sua banca atingiu os $1056.
- O Jogador #4 teve uma performance igualmente fraca. Ao todo jogou 563 rondas e a sua banca atingiu os $1172. A aposta média foi de $14.70 e a aposta máxima atingiu os $50.
- O Jogador #5 teve um percurso semelhante ao Jogador 3. Jogou apenas 517 rondas e a sua banca nunca ultrapassou os $1086. Das 517 rondas, ganhou apenas 236 (45,7%).
Deve ter reparado que eu foquei particularmente os tamanhos das apostas e as percentagens de vitórias e derrotas para a estratégia D'Alembert. Isto porque esta estratégia deve funcionar de tal forma que os jogadores lucram quando ganham o mesmo número de rondas que perdem. No entanto, isso simplesmente não funciona dessa forma na roleta.
Ao todo, os 5 jogadores jogaram 4937 rondas, das quais venceram por 2366 vezes e perderam as restantes 2571. Assim sendo a percentagem geral de vitórias foi de apenas 47,9% Devido ao maior número de rondas perdidas, o tamanho da aposta sobe consistentemente. Isso proporciona também mais oscilações ao longo do tempo.
Estratégia de Labouchere para a roleta
A estratégia de Labouchere é mais complicada que as estratégias mencionadas anteriormente neste artigo. Exige que acompanhe as suas apostas e adicione números, o que pode requerer alguma prática.
A estratégia de Labouchere funciona da seguinte forma:
- O jogador cria uma "linha de apostas", que determinará o tamanho da aposta inicial, bem como o tamanho das apostas nas rondas seguintes, pelo menos até certo ponto. A linha em jogo depende completamente do jogador. Pode ser tão simples como 1-1-1-1-1-1 ou 1-2-3-4-5-6, ou pode ser mais complexo como 1-2-4-4-3-7.
- O jogador utiliza sempre um número em cada extremidade da linha e soma-os. A sua soma determina a quantia apostada nessa ronda.
- Se o jogador perder, coloca no final da linha a soma dos dois números acabou de apostar De seguida volta ao ponto 2 e continua.
- Se o jogador vencer, ele risca da linha os dois números que ele acabou de apostar De seguida volta ao ponto 2 e continua.
- Se o jogador ficar sem números na linha de apostas, poderá começar novamente desde o início ou criar uma linha de apostas diferente.
Eu sei que isto pode parecer um pouco complicado, por isso vamos utilizar um exemplo para clarificar. Confira a tabela abaixo.
| Ronda# | Linha de apostas atual | Montante apostado | Resultado da ronda |
|---|---|---|---|
| 1 | 1-2-3-4-5-6 | 1 + 6 = 7 | DERROTA |
| 2 | 1-2-3-4-5-6-7 | 1 + 7 = 8 | VITÓRIA |
| 3 | 2-3-4-5-6 | 2 + 6 = 8 | DERROTA |
| 4 | 2-3-4-5-6-8 | 2 + 8 = 10 | DERROTA |
| 5 | 2-3-4-5-6-8-10 | 2 + 10 = 12 | VITÓRIA |
| 6 | 3-4-5-6-8 | 3 + 8 = 11 | VITÓRIA |
| 7 | 4-5-6 | 4 + 6 = 10 | ... |
Ao utilizar a estratégia de Labouchere, o seu "objetivo" é ficar sem números na sua linha de apostas. Se conseguir alcançar esse feito, o seu lucro será igual à soma dos números com os quais começou, independentemente do número de vitórias e perdas que obteve ao longo do caminho.
A matemática funciona muito bem com esta estratégia, mas deve ter em mente que as hipóteses estão a favor do casino. Isto significa que a longo prazo esta estratégia não o fará vencer magicamente a roleta.
Vantagens e desvantagens da estratégia de Labouchere
Em termos de risco, a estratégia Labouchere está entre as estratégias de Fibonacci e D'Alembert. A matemática funciona muito bem e terá lucro se conseguir ganhar, pelo menos, o mesmo número de rondas que perder. No entanto, já sabe que não é muito provável que isso aconteça a longo prazo.
Além disso, caso se depare com uma sequência de derrotas, os números na sua linha ficarão cada vez maiores. A sua linha continuará a aumentar e terá que apostar cada vez mais dinheiro. E pior que isso, as apostas continuarão bem grandes altas mesmo depois de começar a ganhar. Precisará de uma longa sequência de vitórias para reduzi-las significativamente.
Simulações da estratégia de Labouchere
As simulações da estratégia Labouchere são bastante complexas, porque dependem da lista de números que os jogadores começam. Para as simulações abaixo, decidi utilizar a linha de apostas seguinte: 1-2-3-4-5-6.
Aqui estão os gráficos:
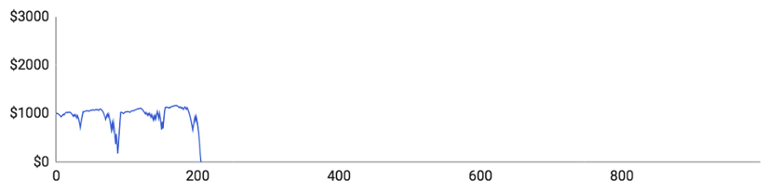
Analisemos a performance individual de cada jogador:
- O Jogador #1 teve de jogar 205 rondas para a sua banca atingir o valor mais alto: $1170. A aposta máxima foi de $240 e a aposta média foi de $44.65 Ele experimentou uma grande perda da qual conseguiu recuperar, mas depois ficou sem dinheiro após uma outra perda.
- O Jogador #2 jogou 227 rondas no total e a sua banca máxima foi de $1296. Em termos de tamanhos de aposta, sua aposta máxima foi de $272 e o valor médio apostado por ronda foi de $28.48.
- O Jogador #3 teve de jogar 350 rondas para a sua banca atingir o valor mais alto: $1504. A sua aposta máxima foi de $377 e a aposta média foi de apenas $27. A sua banca estava crescendo de forma constante, mas um grande declínio fez com que perdesse toda a sua banca.
- O Jogador #4 teve resultados muito interessantes. Ele jogou 996 rondas de roleta, o que é um número significativamente maior do que todos os outros jogadores jogaram. A sua banca atingiu os $2881. Isto porque ele venceu 52,1% das rondas que disputou, o que basicamente significa que ele teve muita sorte. No entanto, apesar de sua taxa de vitória surreal, acabou com $0 depois de uma enorme queda.
- O Jogador #5 teve de jogar 157 rondas para a sua banca atingir o valor mais alto: $1201. A aposta máxima foi de $205 e a aposta média foi de $31.57
Os resultados desta simulação são bastante interessantes, especialmente os resultados do Jogador # 4, que teve uma sequência particularmente boa. As simulações mostram claramente as principais desvantagens da estratégia de Labouchere - as flutuações no montante da aposta causam grandes altos e baixos.
Essa estratégia (com uma linha de aposta inicial 1-2-3-4-5-6) parece ser a mais arriscada entre as quatro estratégias abordadas neste artigo. A banca dos jogadores estava aumentando rapidamente, mas os jogadores também conseguiram perder mais rápido (em média). É claro que isso pode ser muito diferente se eu escolher uma linha de apostas diferente para esta simulação.
As melhores estratégias da roleta
Como teve oportunidade de constatar, abordei neste artigo as razões pelas quais estas estratégias parecem funcionar, mas acabarão por consumir toda a sua banca. É por isso que não recomendo a utilização das mesmas.
Existem estratégias melhores, que podem maximizar as suas hipóteses de sair do casino com lucro, ou pelo menos aproveite para diverte-se o máximo possível enquanto joga. Com isto, não estou a dizer que elas permanecerão lucrativas a longo prazo, mas é o melhor que pode conseguir. Se estiver interessado, leia o meu artigo sobre estratégias que resultam na roleta.